单调栈
一. 定义
下面引自百度百科 > 单调递增或单调减的栈,跟单调队列差不多,但是只用到它的一端,利用它可以用来解决一些ACM/ICPC和OI的题目,如RQNOJ 的诺诺的队列等。
二. 单调栈实现过程
单调栈是一种特殊的栈,特殊之处在于栈内的元素都保持一个单调性。
假设下图是一个栈内元素的排列情况(单调递增的栈):从下到上依次递增
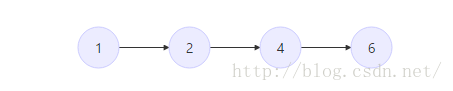
此时插入情况有两种:
- 插入元素大于栈顶元素
当插入7时,因7 > 6,满足单调递增的条件,故可以直接加入栈 此时:
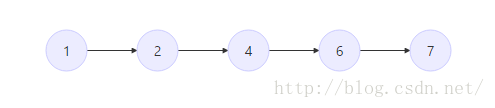
- 插入的元素小于栈顶元素
当插入3时,为了满足单调递增栈的性质,需要先将栈顶的4,6弹出,再插入,此时:
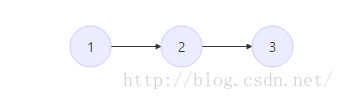
以上的内容和图我相信是非常容易理解的, 但单调栈的作用和功能并不能得到很好的体现, 故下面将用文字 + 图示的形式来展示单调栈的作用
先上结论:
利用单调栈,可以找到从左/右遍历第一个比它小/大的元素的位置
三. 举例
举个例子:
假设有一个单调递增的栈 S和一组数列:
a : 5 3 7 4
用数组L[i] 表示 第i个数向左遍历的第一个比它小的元素的位置
如何求L[i]?
首先我们考虑一个朴素的算法,可以按顺序枚举每一个数,然后再依此向左遍历。 但是当数列单调递减时,复杂度是严格的O(n^2)。
此时我们便可以利用单调栈在O(n)的复杂度下实现
我们按顺序遍历数组,然后构造一个单调递增栈
- i = 1时,因栈为空,L[1] = 0,此时再将第一个元素的位置下标1存入栈中
此时栈中情况:

- i = 2时,因当前3小于栈顶元素对应的元素5,故将5弹出栈 此时栈为空,故L[2] = 0然后将元素3对应的位置下标2存入栈中
此时栈中情况:

- .i = 3时,因当前7大于栈顶元素对应的元素3,故 L[3] = S.top() = 2 (栈顶元素的值)
然后将元素7对应的下标3存入栈 此时栈中情况:
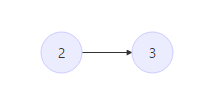
- i = 4时,为保持单调递增的性质,应将栈顶元素3弹出 此时 L[4] = S.top() = 2;
然后将元素4对应的下标3存入栈 此时栈中情况:
至此 算法结束
对应的结果:
a : 5 3 7 4
L : 0 0 2 2
总结:一个元素向左遍历的第一个比它小的数的位置就是将它插入单调栈时 栈顶元素的值,若栈为空,则说明不存在这么一个数。然后将此元素的下标存入栈, 就能类似迭代般地求解后面的元素
四.延伸
有让求每个元素两边的离的最近的比它小的数,这时元素弹出的时候,左边照常收集,不过多收集一组信息R,记录是哪个元素让它弹出的,下标记录到R中,这样L中记录了左边离它最近的比它小的数,R中记录了右边离它最近的比它小的数
特殊情况就是,所有元素都进栈之后,栈中剩余的元素怎么算,只需要将栈中元素依次弹出,正常记录左边的比它小的值的下标,而R数组中,凡是不因元素的进入而弹出,而是因为清空栈自动弹出的元素,所对应的R数组中的值都为空,即不存在。
五. 代码实现
代码实现中只在元素弹出的时候记录它左右两边的值。元素进栈的时候不做任何操作
#include<iostream>
#include<stack>
using namespace std;
int main(){
int a[100];
int L[100];
int R[100];
stack<int> s;
int n;
int temp;
a[0] = 0;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
while(!s.empty() && a[i]<=a[s.top()]){
temp = s.top();
s.pop();
L[temp] = s.top(); //记录它左边的紧挨着的比它小的值
R[temp] = i; //i让它弹出,i就是右边最近的比它小的值,都记录下标的信息
}
s.push(i);
}
while(!s.empty()){
int temp = s.top();
s.pop();
L[temp] = s.top();
R[temp] = 0; //主动弹出,右边没有比它小的,记为空
}
for(int k=1;k<=n;k++){
cout<<"左边最近"<<(L[k]==0 ? 0:a[L[k]])<<" "<<"元素"<<a[k]<<" "<<"右边最近"<<(R[k]==0?0:a[R[k]])<<endl;
}
}
本文参考链接:https://blog.csdn.net/WuBaizhe/article/details/70136174