可见山峰对

题目描述：

一个不含有负数的数组可以代表一圈环形山，每个位置的值代表山的高度，比如｛3，1，2，4，5｝、｛4，5，3，1，2｝或｛1，2，4，5，3｝都代表同样结构的环形山。3->1->2->4->5->3方向叫做next方向(逆时针)，3->5->4->2->1->3方向叫做last方向叫做last方向（顺时针）

山峰A和山峰B能够相互看见的条件为：

1、如果A和B是同一座山，认为互相看不见

2、如果A和B是不同的山，并且在环中相邻，认为可以相互看见

3、如果A和B是不同的山，并且在环中不相邻，假设两座山高度最小值为min。如果A通过next方向到B的途中没有高度比min大的山峰，或者A通过last方向到B的途中没有高度比min大的山峰，认为A和B可以相互看见

给定一个不含负数的数组arr，请返回有多少对山峰可以互相看见

分析：

两座山峰算作一对比如(1，3)和(3，1)是一对 + 假如没有重复的值

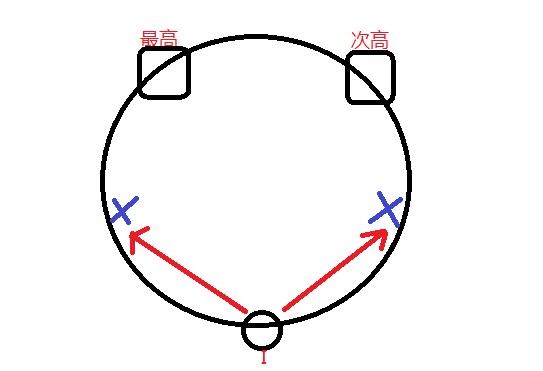
如果有一座山峰，则结果为0，

如果有两座山峰则结果为1，

如果有多座山峰，先找到整个山峰中的最高和次高的山峰，任意一座山峰i，可向两个方向延伸，如果碰到离自己最近的比自己高的就停止，所以从一座山峰出发一定能找到两对，（一对山峰对中我们选择较低的那一个作为开始）一共有n座山，减去最高和次高还剩n-2座山，一定存在2*(n-2)个山峰对可看见，再加上最高和次高那一对，一共存在2*n-3对；

如果有重复值就需要用到单调栈

先找到最大值，压入栈底，同时记录山峰的数量，如果有多个最大值，压入第一个出现的最大的，接着从最大值出发顺时针压入山峰，如果压入的山峰的高度比栈顶的小就压入，如果压入的山峰的高度和栈顶相同，就将栈顶山峰数量加1，如果压入的山峰的高度比栈顶的大，就将栈顶元素弹出，弹出的时候就结算

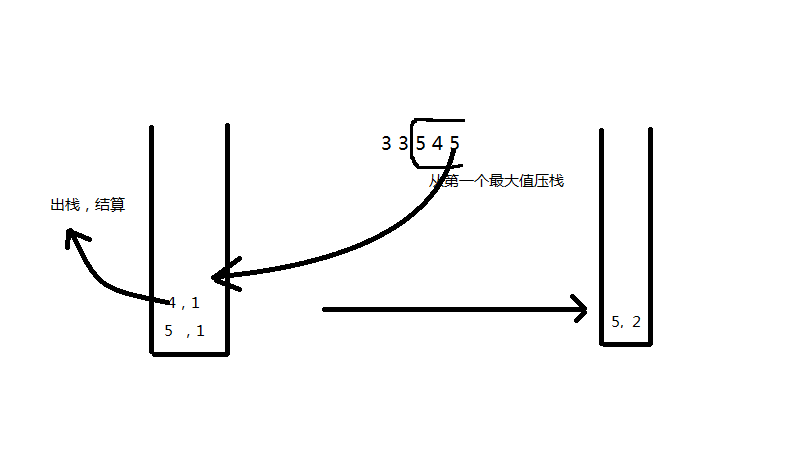
因为是从最大值压入的，所以结算的时候下边一定有比自己大的山峰，右边比自己大的山峰是比自己出栈的那个，结算的规则是：

如果弹出的山峰数量是1 ，结算为两对

如果弹出的山峰的数量为K，结算的结果为k个里面任选两个组成一对共C²_k个，再加上k个山峰到两头最大值的个数2*k个总共是(C²_k+2*k)个

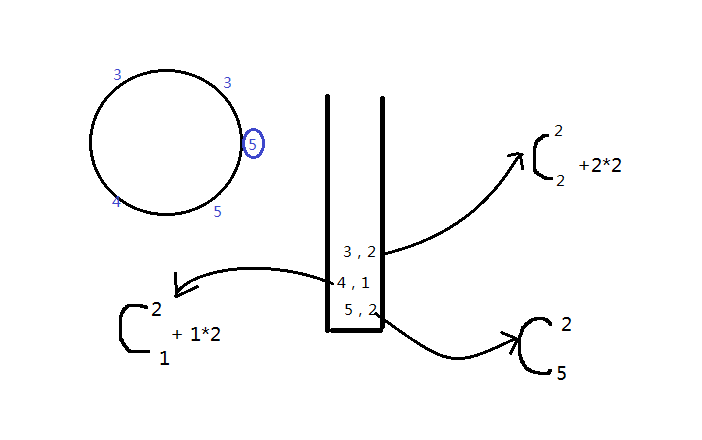
数组遍历完毕栈中还有剩余：若还剩三层及以上，那么三层及以上左边和右边都有最大值(右边最大值为栈底的最大值)，结算为(C²_k+2 * k),

到了最后两层，因为倒数第二层左边最大值和右边最大值是同一个值，都为栈底元素，所以栈底元素的数量就决定了结算的值为多少，若栈底最大元素只有一个则结算为(C²_k+k)个，若栈底最大元素有多个则结算为(C²_k+2 * k)个，

栈底元素结算的时候，栈底元素为最大值结算为C²_k个

至此分析结束，就按照有重复数字来实现

代码实现

#include<iostream>
#include<stack>
#define maxsize 1000
using namespace std;

struct z{   //定义栈中压入的结构
	int data;  //压入的值
	int size;   //值的个数
	z(){
		size=0;
	}
};
stack<z> s;
int a[maxsize];

int jiesuan(int number){   //结算函数
	if(number==1)
		return 2;
	else{
		return number * (number-1) / 2 + number * 2;	}	
}


int in(int a[maxsize],int n,int flag){
	int res=0;
	
	for(int i=flag;i<n;i++){   //从第一个最大值开始压栈
		if(s.empty()){ //栈为空则直接压入，继续执行下一次
			z node4;
			node4.size = 1;
			node4.data = a[i];
			s.push(node4);
			cout<<s.top().data<<"入栈" <<endl;
			continue;
		}
		if(a[i]>s.top().data){   //栈不为空，若要压的元素大于栈顶元素
		while(!s.empty() && a[i]>s.top().data){ //栈顶元素弹出
			z node1;
			node1 = s.top();
			int number = node1.size;
			res += jiesuan(number);  //栈顶元素弹出就结算
			cout<<s.top().data<<"出栈"<<endl;
			s.pop();
			}
			z node5;
			node5.size = 1;
			node5.data = a[i];
			s.push(node5);  //弹出完成后把要压的值压入栈中
			cout<<s.top().data<<"入栈" <<endl;
		}
        //栈顶元素大于要压的值
		else if(!s.empty() && a[i]<s.top().data){ 
				z node;
				node.data = a[i];
				node.size = 1;
				s.push(node);   //直接压入
				cout<<s.top().data<<"入栈" <<endl;		
		}
			
		else if(!s.empty() && a[i]==s.top().data)  
        //栈顶元素等于要压的值，栈顶元素数量加1
				s.top().size++;
		}
	//走到头之后从0开始压入最大值之前的数，操作和上述过程完全一样
	for(int i=0;i<flag;i++){ 
		if(s.empty()){
			z node4;
			node4.size = 1;
			node4.data = a[i];
			s.push(node4);
			cout<<s.top().data<<"入栈" <<endl;
			continue;
		}
		if(a[i]>s.top().data){
		while(!s.empty() && a[i]>s.top().data){
			z node1;
			node1 = s.top();
			int number = node1.size;
			res += jiesuan(number);
			cout<<s.top().data<<"出栈"<<endl;
			s.pop();
			}
			z node5;
			node5.size = 1;
			node5.data = a[i];
			s.push(node5);
			cout<<s.top().data<<"入栈" <<endl;
		}
		else if(!s.empty() && a[i]<s.top().data){
				z node;
				node.data = a[i];
				node.size = 1;
				s.push(node);
				cout<<s.top().data<<"入栈" <<endl;		
		}
			
		else if(!s.empty() && a[i]==s.top().data)
				s.top().size++;
		
	}
	//原数组的元素全部压入栈中，栈中最后有剩余
	while(!s.empty()){
		if(s.size()>=3){ //剩余数量大于3  
			z node2;
			node2 = s.top();
			int number = node2.size;
			res += jiesuan(number); // 弹出结算，规则和压入弹出的规则一样
			cout<<s.top().data<<"出栈"<<endl;
			s.pop();
		}else{
			if(s.size()==2){ //数量等于二
				z node3;
				node3 = s.top();
				cout<<s.top().data<<"出栈"<<endl;
				s.pop();
				if(s.top().size==1){   //看栈底元素的个数 ,只有一个
					res += jiesuan(node3.size)-node3.size;
				}else  //栈底元素的个数多余一个
				{
					res +=jiesuan(node3.size);
				}
			}
			if(s.size()==1){  //只有栈底有元素
				if(s.top().size>1)
					res += s.top().size *( s.top().size-1)/2;//结算
				cout<<s.top().data<<"出栈"<<endl;
				s.pop();
			} 
		}
		
	}
	
	return res;
}


int main(){
	int n;
	cin>>n;
	int max=0;
	int flag;
	for(int i=0;i<n;i++){
		cin>>a[i];
		if(max<a[i]){
			max = a[i];
			flag = i;
		}
	}
	cout<<in(a,n,flag)<<endl;
}

可见山峰对

题目描述：

分析：

代码实现

Ferry