多元线性回归
什么是多元线性回归
我们知道y=ax+b是一元一次方程,y=aX1+bX2+c是二元一次方程.其中,“次”指的是未知数的最大幂数,“元”指的是表达式中未知数的个数(这里就是x的个数).那么”多元”的意思可想而知,就是表达式中x(或者叫自变量,也叫属性)有很多个.
当b=0时,我们说y=ax,y和x的大小始终符合y/x=a,图像上任意一点的坐标,y值都是x值的a倍.我们把这种横纵坐标始终呈固定倍数的关系叫做”线性”.线性函数的图像是一条直线.所以我们知道了多元线性回归函数的图像一定也是一条直线.
多元线性回归就是:用多个x(变量或属性)与结果y的关系式 来描述一些散列点之间的共同特性.
这些x和一个y关系的图像并不完全满足任意两点之间的关系(两点一线),但这条直线是综合所有的点,最适合描述他们共同特性的,因为他到所有点的距离之和最小也就是总体误差最小. 所以多元线性回归的表达式可以写成:
y= w1x1 + w2x2 + w3x3 + … + wnxn
我们知道y=ax+b这个线性函数中,b表示截距.我们又不能确定多元线性回归函数中预测出的回归函数图像经过原点,所以在多元线性回归函数中,需要保留一项常数为截距.所以我们规定
y= w0x0 + w1x1 + w2x2 + w3x3 + … + wnxn
这样多元线性回归函数就变成了:
y= w0 + w1x1 + w2x2 + w3x3 + … + wnxn
如果没有w0项,我们 y= w0 + w1x1 + w2x2 + w3x3 + … + wnxn就是一个由n+1个自变量所构成的图像经过原点的直线函数.那么就会导致我们一直在用一条经过原点的直线来概括描述一些散列点的分布规律.这样显然增大了局限性,造成的结果就是预测出的结果函数准确率大幅度下降.
多元线性回归的推导过程


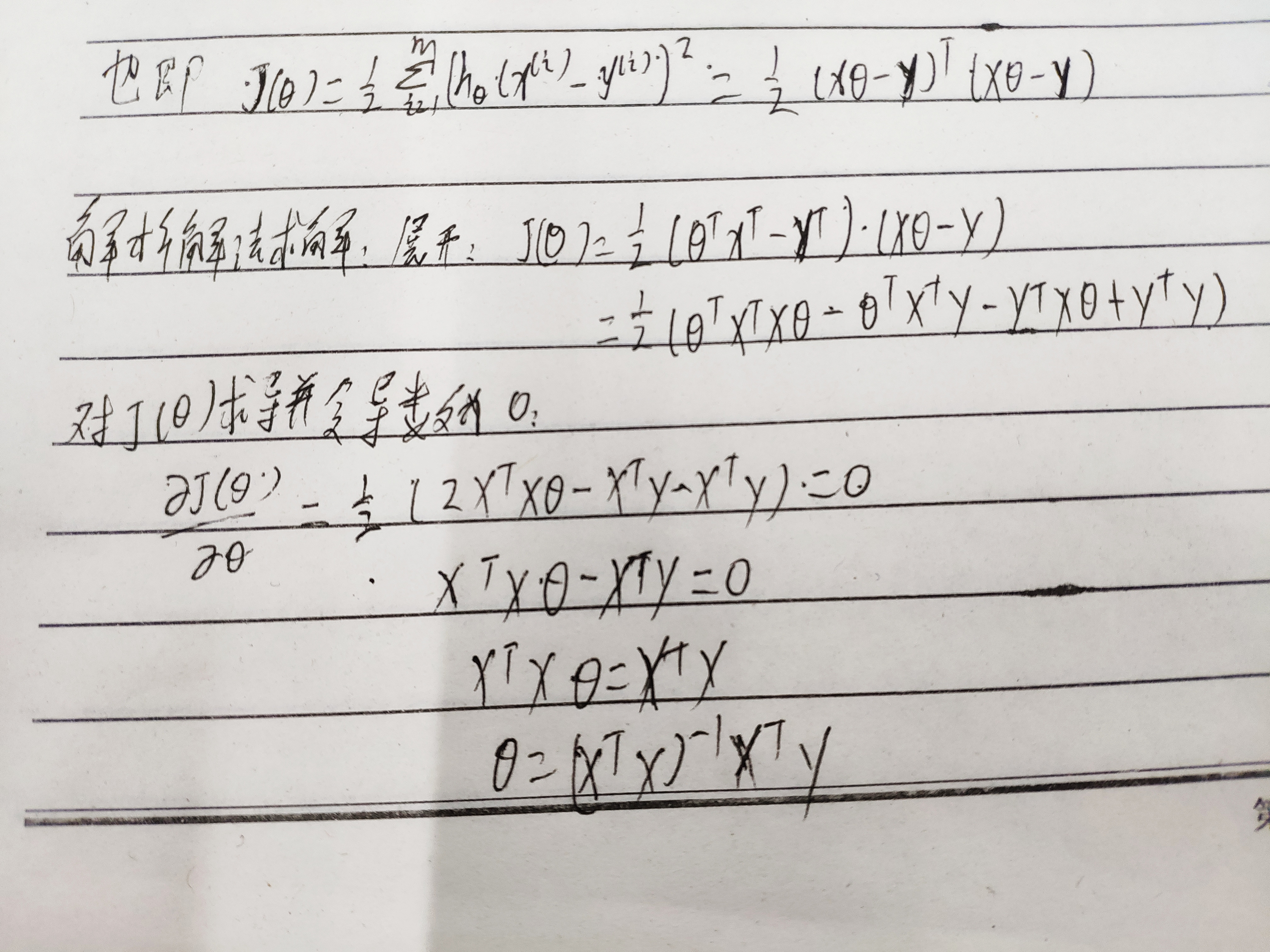
因为在使用解析解求解最小二乘的过程中,出现了矩阵求逆的步骤。因为有些矩阵没有逆矩阵,只能使用近似矩阵来代替,所以结果的精度会降低。二则矩阵求逆随着维度的增加,计算量也大大增加,求解速度变慢。