最大子矩阵
题目:
给定一个整型矩阵map, 其中的值只有0 和 1 两种, 求其中全是1 的所有矩形区域中, 最大的矩形区域为1的数量。
例如:
1 0 1 1
1 1 1 1
1 1 1 0
其中,最大的矩形区域有6个1,所以返回6 。
分析
最大矩形区域的面积怎么求,先来看一个例子,即图中矩形区域的最大面积为多少
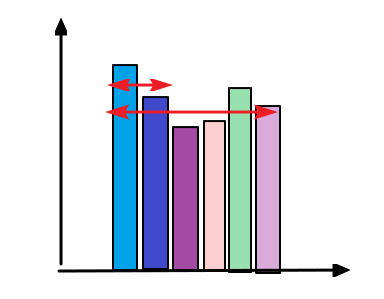
计算的时候以每个直方图为底向两边扩张,遇到比自己大的就扩张,遇到比自己小的就停止,最后看以哪个直方图为底的矩形区域面积最大,这样就计算出最大矩形区域的面积,图中最大矩形区域面积为第三个直方图为底的矩形区域面积,每个直方图的宽度都设为1 矩形区域的面积=直方图的高 X 扩的宽度
同理求子矩阵的最大矩形区域,将矩阵的每列看做一个直方图向两边扩,求出以该列为底的矩形区域的最大面积,扩到不能扩为止,这时求出的就是最大矩形区域
那么问题来了,每列的高怎么计算呢,从矩阵的第零行出发,引入一个数组help用来记录每行的0和1的加和情况,初始化为0,数组的长度等于矩阵的列数,本题中初始化为[0,0,0,0],更新规则为:若该行数字为1则help数组对应位置上数值加一,若该行数字为0,则help数组对应位置上数值直接设为0
第零行的数据为[1,0,1,1],故help[1,0,1,1]
第一行的数据为[1,1,1,1],故help[2,1,2,2]
第二行的数据为[1,1,1,0],故help[3,2,3,0]
计算过程中每算出一组help数组的值,就计算一下最大矩形面积,即每一次计算出help数组,就以该行作为坐标系的X轴,计算最大面积,最大面积不需要存储只需要不断更新
而比较的过程中就需要用到单调栈,将help数组的值压入栈中,因为是遇到小的就停止,所以单调栈顺序是从小到大的,具体讲解见单调栈,每个数值记录了左边第一个比它小的和右边第一个比它小的,只需要让两个值相减就能得到直方图的宽度,再乘以直方图的高度即help数组的值,即可求出该矩形区域的面积,将矩阵遍历一遍就能得出结果
时间复杂度O(m*n)
代码实现
#include<iostream>
#include<stack>
using namespace std;
int maxRecFromBottom(int *help,int n){
if(help==NULL)
return 0;
stack<int> s;
int temp;
int left;
int right;
int lar=-1;
for(int i=0;i<n;i++){
while(!s.empty() && help[i]<help[s.top()]){ //这里等于加不加都一样不会影响弹出时结算的值
temp = s.top(); //记录下标,将要弹出
s.pop(); //弹出
left = s.empty() ? -1 : s.top(); //左边离它最近的
lar = max(lar, (i-left-1) * help[temp]); //算出弹出的那个值扩的宽度乘以弹出的值的高度
}
s.push(i);
}
while(!s.empty()){ //主动弹出,和上述过程一样
int mid = s.top();
s.pop();
left = s.empty() ? -1 : s.top();
lar = max(lar,(n-left-1) * help[mid]);//主动弹出的值右边界是数组的长度,无论右边界是大还是小都会在最后一个
}
return lar;
}
int maxRecSize(int *map,int m,int n){
if(map==NULL||m==NULL||n==NULL)
return 0;
int *help = new int[n];
for (int i = 0; i < n; i++)
help[i] = 0; //初始化为0
int MAX=0;
for(int j=0;j<m;j++){
for(int k=0;k<n;k++){
help[k] = map[j*n+k] == 0 ? 0:help[k]+1; //算出每一行的help数组
}
MAX = max(MAX,maxRecFromBottom(help,n)); //算出help数组的最大值
}
return MAX;
}
int main(){
int m,n;
cin>>m>>n;
int *map = new int[m*n];
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
cin>>map[i*n+j];
}
}
cout<< maxRecSize(map,m,n)<<endl;
return 0;
}