线性回归中的正则化
正则化可以解决模型过拟合的问题,产生过拟合一般有三个原因:
- 训练数据过少
如果数据本身就不够多,无法覆盖真实的数据分布,那么数据训练会对现有的片面数据训练过度
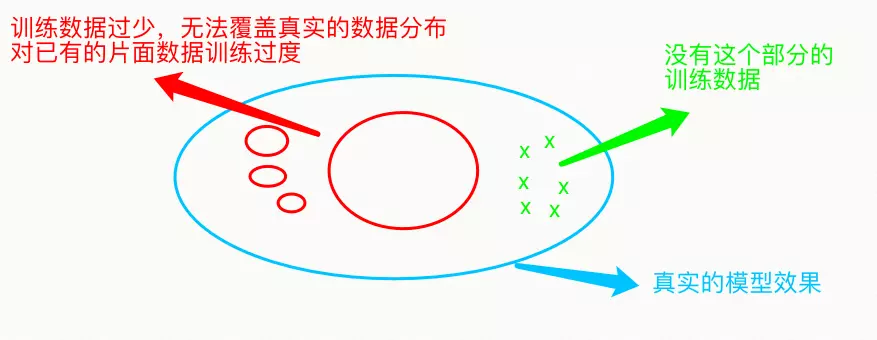
- 数据特征过多(也属于模型过于复杂)
大道至简,虽然影响一件事情的因素有很多,即使是有多元思维模型的人也难以穷尽这些因素,求解模型也一样,总有几个或者没有那么多的特征才值得去重用,其他的权重稍微影响稍微有存在感即可
- 模型过于复杂
人脑善于把复杂的东西,进行归纳和总结,甚至是抽象出“概念”,即是越复杂的东西越难寻根问底,越难的东西不一定越高级、越好,数学公式向来都是美妙而简洁(一般来说)。
正则化的本质是什么?
本质是对权重W的约束。某个特征的权重越小,该特征就越不能起决定作用,改无关紧要的特征只能对模型进行微调,扰动较小,可以让模型专注于有决定性的那些特征。
3.正则化有哪些方法?
在梯度下降推导中,我们希望调整 w,使得损失函数 J(w) 越来越小,所以可以给损失函数添加一个关于w的惩罚项,用来约束w,即J(w)new = J(w)old + H(w)
常见的惩罚项有L2和L1的罚项
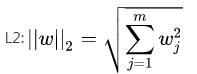
可以防止模型过拟合(overfitting)
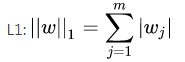
可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择,一定程度上也可以防止过拟合
- 岭回归
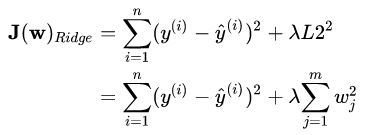
岭回归可以使得某些不重要的权重w变小
- LASSO回归
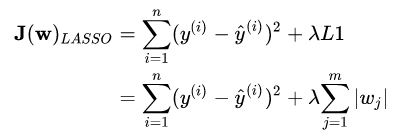
LASSO回归可以使某些权重在训练的过程中变为0 注意:\lambda是需要我们自己指定,是惩罚项的惩罚力度 ,L1本身就有很大的惩罚力度,可以使得某些w为0, 可以进行特征选择。L2常用,模型属于L2的多。
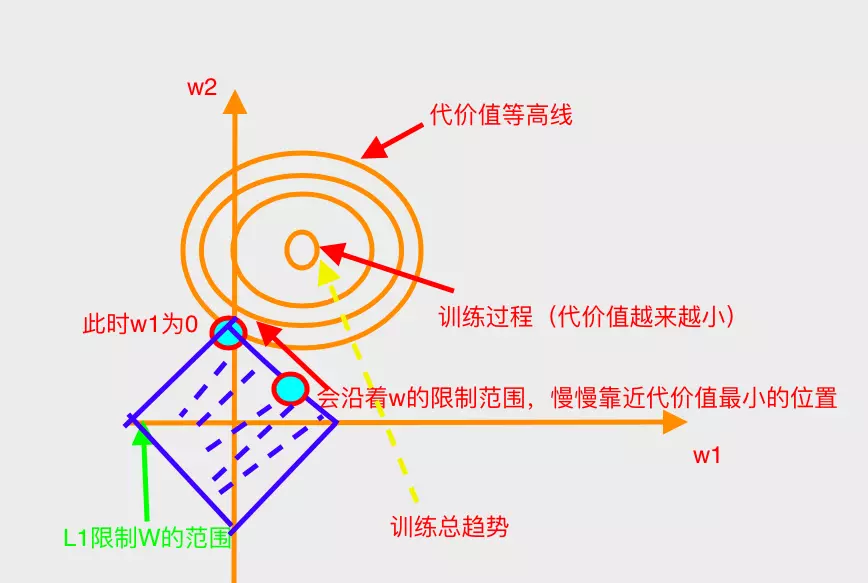
对L1、L2的图解(以2维权值为例)
无惩罚项的梯度下降过程(三维)
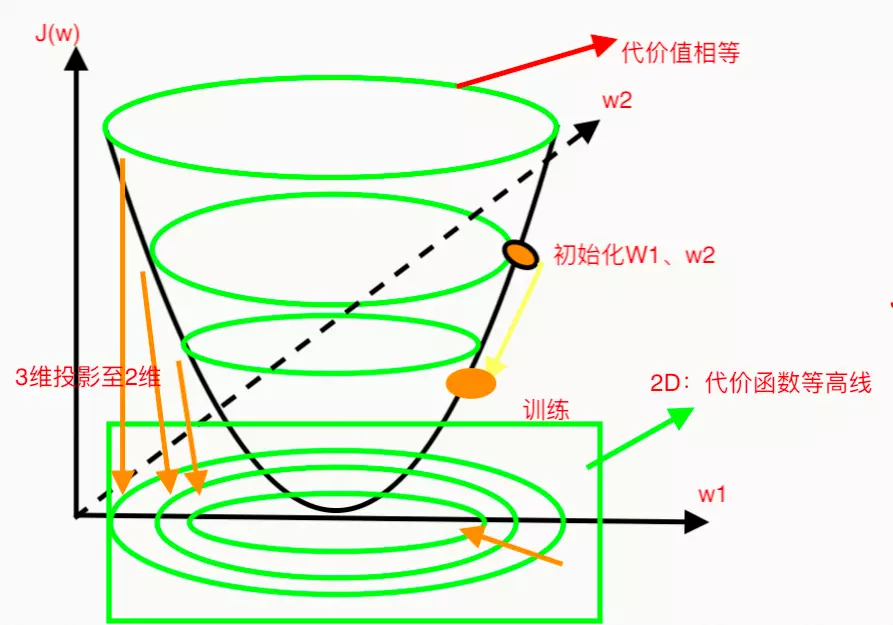
无惩罚项的梯度下降(二维)
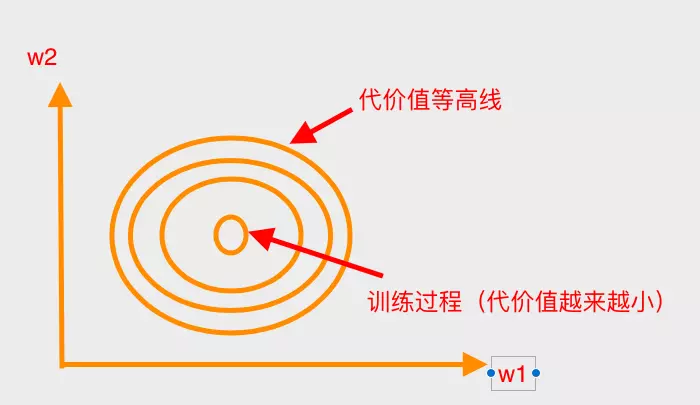
带L2惩罚项的梯度下降(二维)
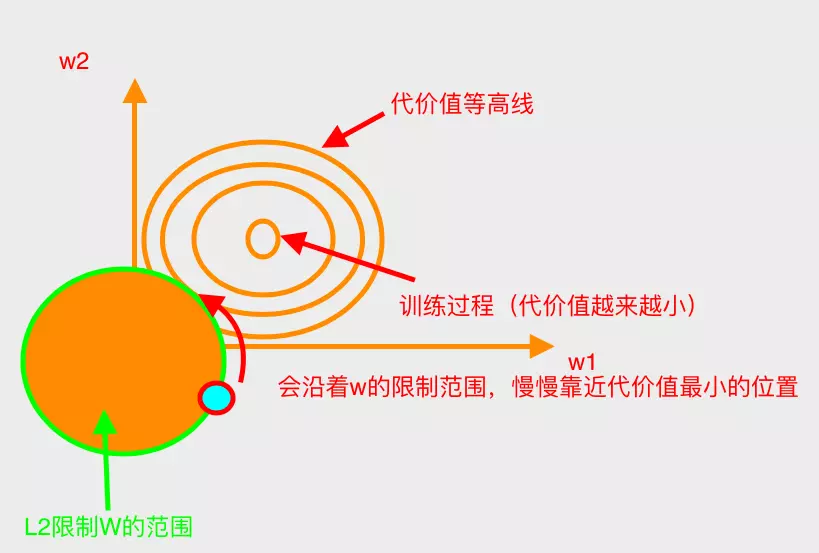
带L1惩罚项的梯度下降(二维)