BFPRT算法

一：背景介绍

在一堆数中求其前 k 大或前 k 小的问题，简称 TOP-K 问题。而目前解决 TOP-K 问题最有效的算法即是 BFPRT 算法，又称为中位数的中位数算法，最坏时间复杂度为O(n) 。

在首次接触 TOP-K 问题时，我们的第一反应就是可以先对所有数据进行一次排序，然后取其前 k 即可，但是这么做有两个问题：

快速排序的平均复杂度为 O(nlogn)，但最坏时间复杂度为 O(n)，不能始终保证较好的复杂度；
我们只需要前 k 大的，而对其余不需要的数也进行了排序，浪费了大量排序时间。

除这种方法之外，堆排序也是一个比较好的选择，可以维护一个大小为 k 的堆，时间复杂度为 O(nlogk)。

先来看一下常规解法：采用快速排序

随机在数组中选择一个数作为划分值（number），然后进行快排的partation过程（将小于number的数放到数组左边，等于number的数放到数组中间，大于number的数放到数组右边），然后判断k与等于number区域的相对关系，如果k正好在等于number区域，那么数组第k小的数就是number，如果k在等于number区域的左边，那么我们递归对左边再进行上述过程，如果k在等于number区域的右边，那我们递归对右边再进行上述过程。

对于常规解法，我们分析一下它的时间复杂度：

递归函数复杂度计算：

T(N)=a*T(N/b)+o(N^d);

当log(b,a) > d时复杂度为O（N^log(b,a）);

当log(b,a) = d时复杂度为O（N^d*log(2,N));

当log(b,a) < d时复杂度为O（N^d);

N为样本数据个数即数组中元素的个数。

N/b为将这N个数划分为更小的部分，每个部分的样本数据个数，一般为均分，那么b等于2。 a为划分为多个部分后，小部分执行的次数。 d为递归函数调用完成后剩下的操作的时间复杂度。

对于最好的情况：每次所选的number正好在数组的正中间，那么上式中a等于1，b等于2，对于partation过程，时间复杂度是O（n），所以d等于1。所以T（N）= T（N/2）+ O（N），此时 log( 2 , 1 ) < 1，故时间复杂度为O（N）。

对于最坏情况：每次所选的number正好在数组最边上，那么时间复杂度为O（N ^ 2）.

BFPRT算法的优化

bfprt算法就是在这个number上做文章，bfprt算法能够保证每次所选的number在数组的中间位置，那么时间复杂度就是O（N）。

第一步：我们将数组每5个相邻的数分成一组，后面的数如果不够5个数也分成一组。

第二步：对于每组数，我们找出这5个数的中位数，将所有组的中位数构成一个median数组（中位数数组）。

第三步：我们再求这个中位数数组中的中位数，此时所求出的中位数就是那个number。

第四步：通过这个number进行partation过程，下面和常规解法就一样了。

接下来我们分析一下为什么bfprt算法每次选number的时候都能够在数组的中间位置。

我们假设这就是分出来的每5个数的小组，每一列代表一个小组。

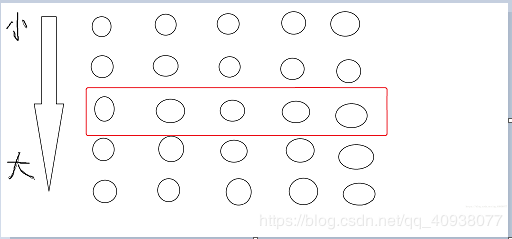
图中红框内的数我们假设就是每一组的中位数。我们假设总数组的数字个数是N，那么中位数数组中数字的个数就是 N / 5 。

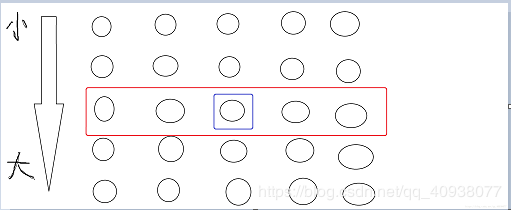
我们假设用蓝框框起来的数是中位数数组的中位数（divide），那么由中位数的性质可知，中位数数组中有一半的数比这个divide大，所以总共有 N / 10个数比这个divide大。

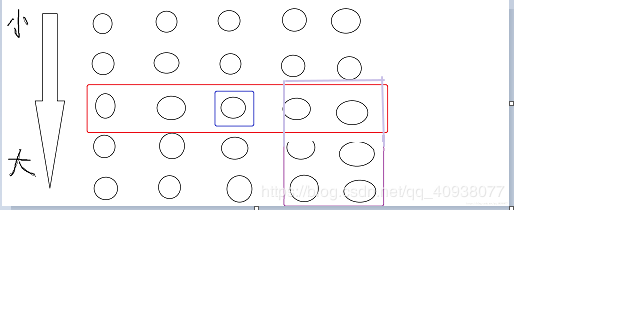
用紫色框框出的数肯定也是比divide大，所以至少有N / 10 + ( 2*N ) / 10 = ( 3*N ) / 10 个数比divide大，那么以divide为划分的partation过程能够使得divide在数组的靠近中间的位置，最坏情况也能够在数组的 ( 3*N ) / 10 或者 ( 7*N ) / 10 的位置。

BFPRT算法的复杂度

number找出来以后分析一下时间复杂度：

分组 O(1)
组内排序 O(n)
重新组合成大小为n的数组 O(n)
BFPRT调用自己 O(n/5)
作为划分值，找中位数 O(n)
若没命中，最坏O(7*n/10)

最坏时间复杂度为：

T(N) = O(1)+O(n)+O(n)+O(n/5)+O(n)+O(7*n/10)=O(N)+O(N/5)+O(7*N/10) 数学上已经证明T(n)=O(n)

到此我们已经将复杂度降到了O(n)

代码实现

完整代码:

#include<iostream>
#include<algorithm>
using namespace std;
int a[2];
int bfprt(int root[],int begin,int end,int k);//这是核心函数，表示在root数组的begin位置到end位置上找出第k小的元素
int getmedian(int root[],int beginI,int endI)//这个函数求的是在root数组中beginI位置到endI位置上的中位数（其实就是求由每5个数所分成的小组的小组内的中位数）
{
    sort(root+beginI,root+endI+1);  //sort函数左闭右开 
    int sum=beginI+endI;
    int mid=(sum/2)+(sum%2);//这个地方加上sum%2是为了确保偶数个数时我们求的是中间两个数的后一个,加不加无所谓，取哪个都一样 
    return root[mid];
}
int medianOfMedians(int root[],int star,int finish)//这个函数是将root数组star位置到finish位置分成每5个数一个小组，并求出每个小组内的中位数
{
    int num=finish-star+1;//求出长度
    int offset=num%5==0?0:1;//最后如果剩余的数不足5个，我们也将其分成一个小组，和前面同等对待
    int range=num/5+offset;
    int median[range];//这个数组存的是每个小组内的中位数
    for(int i=0;i<range;i++)//依次往median数组中填数
    {
        int beginI=star+i*5;//第i组数对应root数组上的位置
        int endI=beginI+4;  //五个一组 
        median[i]=getmedian(root,beginI,min(endI,finish));
    }
    return bfprt(median,0,range-1,range/2);//求出生成好的median中位数数组，利用Bfprt求出number值，作为partation函数的划分值
}
void swap(int root[],int a,int b)
{
    int temp=root[a];
    root[a]=root[b];
    root[b]=temp;
}
void partation(int root[],int beginJ,int endJ,int number)//partation函数求的是等于number的范围
{
    int less=beginJ-1;
    int more=endJ+1;
    int cur=beginJ;
    while (cur<more)
    {
        if(root[cur]<number)
        {
            less++;
            swap(root,cur,less);
            cur++;
        }
        else if(root[cur]==number)
            cur++;
        else
        {
            more--;
            swap(root,cur,more);
        }
    }
    a[0]=less+1; //小于区域的右边界，加一是为了防止溢出 
    a[1]=more-1; //大于区域的左边界，减一是为了防止溢出，
				//而且下面判断范围时加了= ，可以保证不会溢出的同时可以判断大小 
}
int bfprt(int root[],int begin,int end,int k)
{
    if(begin==end)//数组中只有一个数时，直接返回
        return root[begin];
    int divide=medianOfMedians(root,begin,end);//求出以哪个数作为划分值
    partation(root,begin,end,divide);//注意，进行完partation过程后，root数组已经呈现出小中大的顺序 
    if(k>=a[0]&&k<=a[1])//如果需要求的数正好在等于区域，直接返回root[k]
        return root[k];
    else if(k<a[0])//此时我们要找的数比divide小，递归求前半部分
        return bfprt(root,begin,a[0]-1,k);   //刚才加上的要减去 
    else if(k>a[1])//此时我们要找的数比divide大，递归求后半部分
        return bfprt(root,a[1]+1,end,k);   //刚才减去的要加上 
}
int main()
{
    int n,k;
    int root[100000];
	cin>>n; 
	cin>>k;
    for(int i=0;i<n;i++)
        cin>>root[i];
    cout<<"第"<<k<<"小的数是"<<bfprt(root,0,n-1,k-1)<<endl;  //k-1是因为数组下标从0开始 
	cout<<"变换后的数组"<<endl; 
    for(int k=0;k<n;k++)
        cout<<root[k]<<" ";
}

本文章在https://blog.csdn.net/qq_40938077/article/details/81213820文章上稍加修改，感谢原作者分享

BFPRT算法

一：背景介绍

BFPRT算法的优化

BFPRT算法的复杂度

代码实现

Ferry